| For such
optical system there is an equation: -1/d1 + 1/d2 = 1/fR
(2.1)
d1 . d2 = fR.d1 - fR.d2
(2.2)
For extendending factor of focal reducer
lentgh there is:
FE
= d2 / d1
(2.3)
So from (2.2) and (2.3) there is:
FE = 1 - d2 / fR (2.4)
FE = fR / (fR + d1) (2.5)
The result focal length
of telescope with objective with fO
is:
f = fO . FE = fO . (1 - d2 / fR) (2.6)
If reducing factor of
focal reducer is N (thus FE
= N), then
d2 = (1 - N) . fR (2.7)
d1 = (1/N - 1) . fR (2.8)
For given lens with fR (and d2 calculated according to
2.7) the next equation can be useful:
d1 = fR.d2 / (fR - d2) (2.9)
|
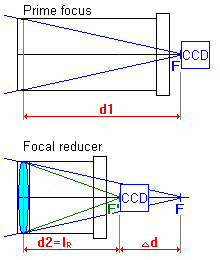 Distance between CCD position in
prime focus and CCD position in focus with focal
reducer is Dd:
Dd = d1 - d2
= d2 / N - d2 = d2 . (1/N - 1)
As d2
= lR
(lR
is distance between focal reducer lens and CCD),
then
Dd = lR . (1/N - 1) (2.10)
Using (2.9) we get:
Dd = lR2 / (fR - lR) (2.11)
|